平成27年度 秋 基本情報技術者試験 【問2】

ソフトⅡコース担当　ブログのおにーさまこと高橋です。

昨日の情報技術者試験、手ごたえはどうだったでしょうか。合格発表は、基本情報約1か月後、それ以外約2か月後です。楽しみに待ちましょう。

では、早速、今回は平成27年度秋期基本情報技術者試験午後問2の解説です。

浮動小数点数の問題です。設問間でヒントになることがあったりします。

設問1
10進数0.625を2進数に変換すると

• (0.101)₂

です。仮数部は、整数部が1になるようにします。これを正規化といいます。データベースにも正規化という言葉があります。混同することはないと思いますが、気を付けましょう。正規化すると、

• (1.01)₂ × 2^-1

です。問題の説明(2）より、指数部には実際の指数に127を加えた値が設定されます。指数部は-1 + 127 = 126です。16進数に変換すると(7E)₁₆となり、正解はイです。

設問2
仮数部は正規化されているので、1を加えて1.1です。指数部は(7E)₁₆で、設問1ができていれば計算するまでもなく-1であることがわかります。(126 – 127= -1)

• (1.1)₂ × 2^-1 = (0.11)₂ = 0.75

正解はオです。

設問3
浮動小数点数の加算は、指数を合わせると、仮数部の加算になります。このとき、指数部の大きいほうに合わせるようにします。Aは問題にあるように

• (1.1)₂ × 2⁵

です。Bの指数部は、(10000011)₂=131です。127を引くと、指数は4になります。と計算しましたが、実は計算しなくても求まります。Aの指数部は(10000100)₂、Bの指数部は(10000011)₂で、BはAより1小さいです。問題よりAの指数は5なので、Bの指数は4であるとわかります。符号部が1なので、Bは負の数です。以上よりBは

• -(1.1)₂ × 2⁴ = -(0.11)₂ × 2⁵

です。加算は

• (1.1)₂ × 2⁵ + (-(0.11)₂ × 2⁵ = ((1.1)₂ + (-(0.11)₂)) × 2⁵ = (0.11)₂ × 2⁵ = (1.1)₂ × 2⁴

となります。空欄aにはオ、空欄bにはイが入ります。仮数部の加算を図示すると次のようになります。

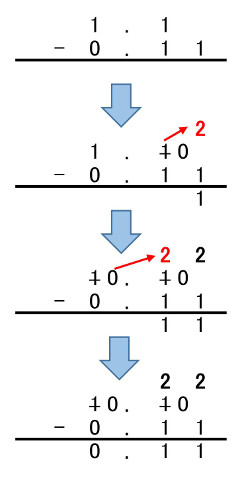
問題にはありませんが、2進数の乗算は、仮数部を掛けて、指数部を加算します。

設問4
A × 10は

• A × 10 = A × (8 + 2) = A × 8 + A × 2

と変形できます。問題よりA × 8=(1.1)₂ × 2⁸です。A × 2は

• A × 2=(1.1)₂ × 2⁵ × 2¹ = (1.1) × 2⁶

です。この2つを加算します。指数を大きいほうに合わせて計算すると、

• (1.1)₂ × 2⁸ + (1.1)₂ × 2⁶ = (1.1)₂ × 2⁸ + (0.011)₂ × 2⁸ = (1.111)₂ × 2⁸

です。指数が8なので、指数部は127加えて135 = (10000111)₂です。これも、Aの指数5より3大きいので、Aの指数部(10000100)₂に(11)₂を加えて求める方が簡単でしょう。仮数部は、整数部の1を除いた111000000…0になります。空欄cにはウが入ります。

できなかったと思われる問題を中心に、再度解いておきましょう。

2015年（平成27年度）秋期の解説

• 平成27年度 秋 基本情報技術者試験 【問1】
• 平成27年度 秋 基本情報技術者試験 【問8】
• 平成27年度 秋 基本情報技術者試験 【問7】
• 平成27年度 秋 基本情報技術者試験 【問6】（その2）
• 平成27年度 秋 基本情報技術者試験 【問6】（その1）
• 平成27年度 秋 基本情報技術者試験 【問5】
• 平成27年度 秋 基本情報技術者試験 【問3】
• 平成27年度 秋 基本情報技術者試験 【問4】（その2）
• 平成27年度 秋 基本情報技術者試験 【問4】（その1）
• 平成27年度 秋 基本情報技術者試験 【問12】
• 平成27年度 秋 基本情報技術者試験 【問2】

Date：

2015.10.19

この記事を
友だちに教える

LINE

TWITTER

- Facebook

- HatenaBookmark

GooglePlus